Nesse artigo será abordado o PID Digital, controlador e algoritmo PID, mencionando conceitos sobre o assunto, e destacando as fórmulas e cálculos.
Controlador PID
O advento dos microprocessadores trouxe uma perspectiva interessante à implementação de controladores PID para controle de processos industriais.
A diferença ao implementar um controlador em um computador digital é que ao invés de trabalhar com sinais contínuos, o controlador toma da saída do processo uma sequência de valores a intervalos de amostragem ∆t e gera uma sequência de valores do sinal de saída. O algoritmo PID deve ser aproximado por uma fórmula discretizada.
Quando uma estratégia de controle por realimentação é implementada digitalmente, a entrada e a saída do controlador devem ser sinais digitais (ou amostrados) ao invés de sinais contínuos (ou analógicos).
Assim, o sinal contínuo do transmissor é amostrado e convertido periodicamente para um sinal digital através de um conversor analógico para digital (ADC). Um algoritmo de controle digital é então usado para calcular a saída do controlador, que é um sinal digital.
Antes da saída do controlador ser enviada para um elemento final de controle, esse sinal é convertido para um sinal contínuo correspondente, através de um conversor digital para analógico (DAC).
Alternativamente, o sinal digital pode ser convertido para uma sequência de pulsos representando a mudança na saída do controlador, os quais são então enviados diretamente a um elemento final de controle, que utiliza entrada de pulsos para mudar sua posição. Válvulas de controle acionadas por motores de passo pulsados são frequentemente usadas com controladores digitais.
O Algoritmo PID Digital
A expressão do PID analógico é mostrada abaixo:
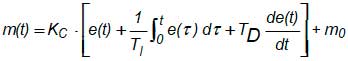
Numa primeira aproximação pode-se escrever o algoritmo PID Digital aproximando-se a integral por uma somatória (aproximação do tipo “retangular para trás”) e a derivada por uma diferença de 1ª ordem (aproximação do tipo “backward difference”):

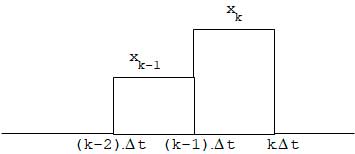
Em realidade, esta aproximação para a integral supõe que a variável medida permaneça constante durante o intervalo de amostragem ∆t e, por isso, ela é chamada de integração retangular (vide figura 1). Pode-se entender esta aproximação do seguinte modo: chamando l(k) a integral do sinal x no instante k, tem-se que l(k)=l(k-1)+ ∆t.x(k).
Chega-se então à seguinte expressão para o controlador PID Digital:
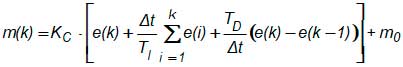
ou, equivalentemente:
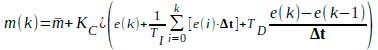
Onde:
∆t= intervalo de amostragem (intervalo de tempo entre amostragens sucessivas da variável controlada)
m(k)= saída do controlador no k-ésimo instante de amostragem, k=1, 2, …
e(k)= desvio no k-ésimo instante de amostragem
Em termos de transformada Z resulta:
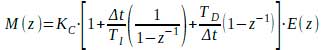
Este algoritmo calcula todas as vezes o valor pleno da saída m(k), sendo chamado PID “posicional”, pois a saída do controlador corresponde à posição do elemento final de controle. Normalmente se utiliza o algoritmo denominado “variacional”, “incremental” ou “de velocidade”, que calcula o valor do incremento ∆m(k) em cada amostragem, conforme mostrado a seguir.
![]()
Computando a equação (12.1) no instante (k-1) tem-se:
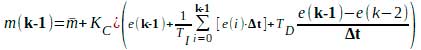
Resulta então:
![]()
que é o algoritmo PID incremental ou de velocidade, no qual a variação na saída do controlador é calculada. A transformada Z deste algoritmo fica:
![]()
Pode-se, no entanto, utilizar a integração trapezoidal, conforme mostrada na figura 2 que é uma aproximação consideravelmente mais precisa para a integral.
![]()
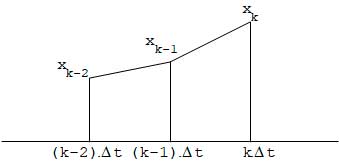
Fig. 2 Integração trapezoidal
Neste caso, o termo integral se torna:
![]()
A forma de velocidade fica:
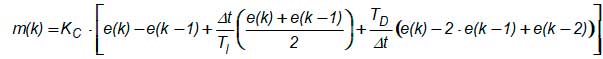
Em termos de transformada Z resulta:
![]()
Além das opções vistas anteriormente para o cálculo do modo integral, existem também opções para o cálculo do modo derivativo, como a mostrada a seguir:
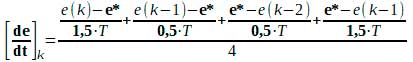
onde:
![]()
Forma Posicional e Incremental
Comparando-se a forma posicional com a forma incremental, resulta (SEBORG et al., 1989):
A forma incremental inerentemente contém alguma proteção contra a saturação do modo integral, pois a somatória dos erros não é explicitamente calculada;
A saída ∆m(k) está em uma forma para utilização direta por elementos finais de controle que requeiram uma entrada incremental, como ocorre em válvulas acionadas por motor de passo;
A forma incremental não requer a especificação do valor de m. Na prática, o valor de m para a forma posicional ou m(-1) para a forma incremental é feito igual ao sinal para o elemento final de controle no instante da transferência manual para automática, pois se assume que é usual a operação manual do controlador preceder sua operação no modo automático; e
Na forma incremental é sempre necessária a inclusão do modo integral, pois o valor de referência r se cancela tanto nas expressões do modo proporcional quanto derivativo, exceto momentaneamente quando uma mudança em r é efetuada. Assim, aplicar a forma de velocidade sem incluir o modo integral poderia levar a variável controlada a se afastar do “set point”.
Eliminação da Saturação do Modo Integral
As seguintes características ocorrem nos controladores PID digitais (SEBORG et al., 1989):
No controlador com forma posicional a saturação do modo integral pode ocorrer quando a somatória do erro cresce a um valor muito alto. Suponha que a saída do controlador esteja em um limite alto ou baixo, como resultado de um sinal sustentado de erro de grande magnitude.
Muito embora a variável medida eventualmente alcance seu “set point” [e(k)=0], o controlador permanecerá em seu limite até que o erro mude de sinal, reduzindo o valor da somatória. Essa situação conduz a um sobressinal excessivo da variável controlada e à saturação da variável manipulada.
Pode-se reduzir o problema de saturação do modo integral no algoritmo posicional, colocando-se um limite superior no valor da somatória. Quando o controlador satura, suspende-se a somatória até que a saída do controlador se afaste do limite.
Note que na forma incremental, nenhuma somatória aparece, evitando o problema de saturação. No entanto, o algoritmo deve ser programado para desconsiderar ∆m(k) se m(k) está no limite, implicando que m(k) deve ser monitorado em cada instante. Na maioria das situações onde o modo integral está presente, o algoritmo de velocidade é preferido ao de posição.
Eliminação do Salto Derivativo
Quando se altera o “set point” em um controlador com o modo derivativo, os algoritmos posicional e incremental produzem uma grande alteração imediata na saída (um impulso). Há alguns métodos disponíveis para eliminar esse efeito:
Ao invés de derivar o desvio e(k), deve-se derivar a variável medida. Assim, ao invés de usar e(k)=r(k)-b(k), deve-se derivar -b(k), resultando:
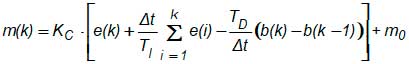
(forma posicional)
![]()
(forma incremental)
Ao invés de mudar o “set point” de forma brusca, rampeie-o, limitando a taxa de variação de r(k).
Se ruído na medição combinado com uma razão grande de tempo derivativo sobre período de amostragem (TD/∆t) está causando um modo derivativo por demais ativo, filtre o sinal de medição antes de calcular a ação derivativa.
Efeito da Saturação no Desempenho do Controlador
Uma das dificuldades que surge ao se usar a forma posicional do algoritmo de controle é que uma pequena alteração no desvio “e” pode levar a saída do controlador a saturar, para alguns valores de seu ajuste. Assim, suponha que KC.TD/∆t=100 devido a um pequeno período de amostragem e que e(k) e m(k) estejam previstos para variar de 0 a 100%.
Uma pequena alteração em ∆e(k)=e(k)-e(k-1) de 1% produzirá uma alteração de 100% em m(k), excedendo seu limite superior. Portanto, deve-se ser cuidadoso ao selecionar os ajustes do controlador e o valor de ∆t, que não cause problemas de saturação.
Algoritmos de Posição e Velocidade
A forma posicional do algoritmo PID requer o valor m0, enquanto a forma incremental não requer explicitamente um valor em estado estacionário para a saída do controlador. No entanto, a inicialização de ambos os algoritmos é igualmente simples, visto que a operação manual do sistema de controle usualmente precede a transferência para o modo automático.
Presumivelmente, o elemento final de controle foi colocado na posição apropriada durante o procedimento de partida em manual, de forma que m0 (ou m(k-1) para o algoritmo de velocidade) é simplesmente igualado ao sinal para o elemento final de controle no instante da transferência;
A forma incremental evita a saturação do modo integral (reset wind up), pois a soma dos erros não é explicitamente calculada;
A saída ∆m(k) está em uma forma pronta para ser usada diretamente por elementos finais de controle, que requerem uma entrada especificando mudança na posição, tal como ocorre em válvulas acionadas por um motor de passo pulsado.
Alguns tipos de estratégias avançadas de controle, tal como controle em cascata, frequentemente requerem que a saída do controlador m(k) seja explicitamente calculada. Caso se opte por utilizar um controlador do tipo incremental, pode-se adotar a seguinte solução:
m(k)=m(k-1)+ ∆m(k)
Uma desvantagem da forma incremental é que o modo integral deve ser incluído. Note que o “set point” se cancela tanto no modo proporcional quanto derivativo na forma incremental, exceto momentaneamente após uma mudança no “set point”. Assim, a aplicação da forma de velocidade sem incluir o modo integral poderia levar a variável controlada a se afastar do “set point”.
Se a variável medida b(k) e o sinal de saída m(k) são computados em termos percentuais ou têm a mesma unidade de engenharia (por exemplo mA ou V), KC deve ser adimensional. No entanto, onde os sinais de entrada e/ou saída do controlador são convertidos internamente em unidades de engenharia, o valor de KC não pode ser adimensional.
Referências Bibliográficas
SEBORG, D. E.; EDGAR, T. F.; MELLICHAMP, D. A. Process dynamics control. New York, John Wiley & Sons, 1989.

